
7 The Order & Complexity Toolbox for Aesthetics (OCTA): A systematic approach to study the relations between order, complexity, and aesthetic appreciation
Van Geert, E., Bossens, C., & Wagemans, J. (2022). The Order & Complexity Toolbox for Aesthetics (OCTA): A systematic approach to study the relations between order, complexity, and aesthetic appreciation. Behavior Research Methods. https://doi.org/10.3758/s13428-022-01900-w
Paper Postprint Figshare Python toolbox Shiny application Additional resources
Abstract
Do individuals prefer stimuli that are ordered or disordered, simple or complex, or that strike the right balance of order and complexity? Earlier research mainly focused on the separate influence of order and complexity on aesthetic appreciation. When order and complexity were studied in combination, stimulus manipulations were often not parametrically controlled, only rather specific types of order (i.e., balance or symmetry) were usually studied, and/or the multidimensionality of order and complexity was largely ignored. Progress has also been limited by the lack of an easy way to create reproducible and expandible stimulus sets, including both order and complexity manipulations. The Order & Complexity Toolbox for Aesthetics (OCTA), a Python toolbox that is also available as a point-and-click Shiny application, aims to fill this gap. OCTA provides researchers with a free and easy way to create multi-element displays varying qualitatively (i.e., different types) and quantitatively (i.e., different levels) in order and complexity, based on regularity and variety along multiple element features (e.g., shape, size, color, orientation). The standard vector-based output is ideal for experiments on the web and the creation of dynamic interfaces and stimuli. OCTA will not only facilitate reproducible stimulus construction and experimental design in research on order, complexity, and aesthetics. In addition, OCTA can be a very useful tool in any type of research using visual stimuli, or even to create digital art. To illustrate OCTA’s potential, we propose several possible applications and diverse questions that can be addressed using OCTA.
The Order & Complexity Toolbox for Aesthetics (OCTA)
7.1 Introduction
Order, complexity, and the balance between order and complexity have long been considered important factors influencing aesthetic appreciation (for a review, see Van Geert & Wagemans, 2020). Although most empirical work has confirmed the importance of order and complexity, concrete results on the extent and direction of order and complexity influences, as well as the relationship between order and complexity, vary widely. Previous research has some limitations concerning the stimuli and manipulations used, however, and leaves some important research options uncovered (cf. The need for OCTA below). The Order & Complexity Toolbox for Aesthetics (OCTA) fills these gaps by providing researchers an easy, open, and reproducible way to create stimuli varying in order and complexity on multiple element features (see Figure 7.1) for some OCTA example stimuli). Being available as both a Python package and a Shiny application, OCTA1 is accessible to both researchers with and without programming experience.
We will first discuss how we define order and complexity, and explain how we view the relation between order, complexity, and appreciation. Next, we list existing stimulus sets and stimulus generation tools (to be) used in research on the perception and appreciation of order and complexity, point out the limitations to the existing research and tools, and indicate how OCTA can provide a fulfilling answer to the existing gaps. Then, we introduce the newly created stimulus generation toolbox and discuss its steps, concepts, and options in more detail. Afterwards, we treat more advanced uses of OCTA, provide a range of potential applications for OCTA, list some possible future extensions of OCTA, and give advice on how to start using OCTA.
7.1.1 Defining order and complexity
In this work, we define (stimulus) order as all aspects related to the structure and organization of information (in a stimulus) and (stimulus) complexity as all aspects related to the quantity and variety of information (in a stimulus; Van Geert & Wagemans, 2020). For example, Figure 7.2a and b have the same number of distinguishable elements and the same dissimilarity between those elements (i.e., complexity; Berlyne, 1960) but differ in the way the elements are arranged (i.e., order). Similarly, also Figure 7.2c and d share the same level of complexity, but differ in the way the elements are organized. In Figure 7.2a and b, the difference in order is a qualitative difference, a difference in the type of order applied. In Figure 7.2c and d, it concerns a quantitative difference, a difference in the level of order present. Figure 7.2a and c have the same overall organization (i.e., level and type of order), but differ in the quantity and variety of information present (i.e., different level of complexity).
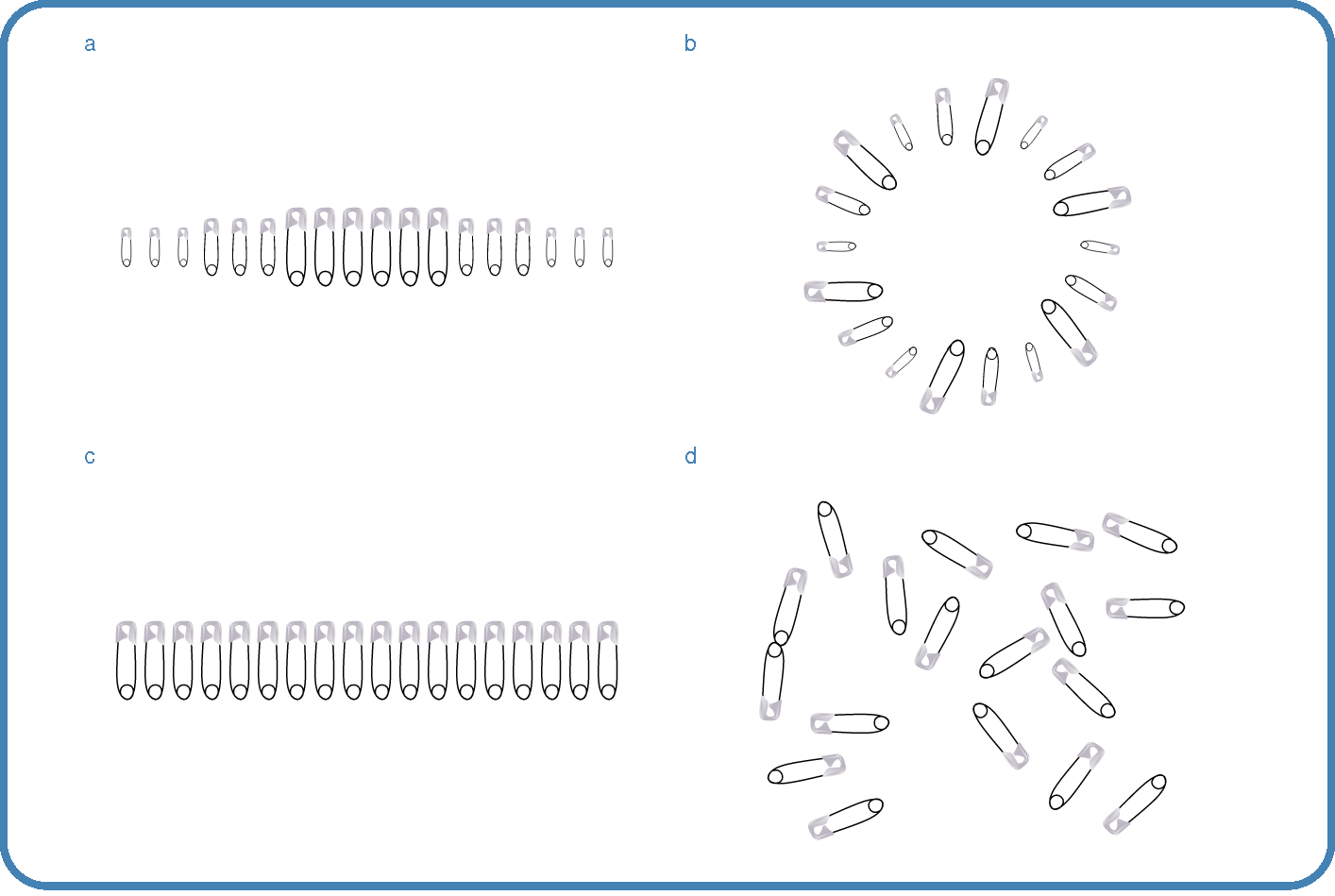
In this example, we referred to the multidimensional concepts of element order and element complexity as referring to a combination of order and complexity on the color, shape, and size dimensions: we focused on the order and complexity of the distinguishable elements present in the stimulus on the different feature dimensions in combination. It is however also possible to investigate other forms of order and complexity in the stimulus, for example position order and complexity, specific feature order and complexity, or the complexity of individual feature values used. Qualitatively different position patterns can be used to place the elements in the stimulus (i.e., type of position order), and these positions can also show more or less diversity (e.g., equally-spaced positions in rows and columns versus completely random positions; position complexity). Feature order and complexity are part of element order and complexity, but focus on one specific element feature at a time. For example, Figure 7.2a has a higher level of size complexity than Figure 7.2c, but Figure 7.2b and d have a higher level of orientation complexity. Furthermore, the individual feature values of the elements present in the stimulus, or the features of the stimulus as a whole, may be more or less complex. For example, a safety pin may be a more complex shape than a circle, or placing the elements on a circular outline may form a less complex overall organization than placing them on a rectangular outline. Acknowledging the multidimensionality of order and complexity may be important in the search for more consistent relationships between order, complexity, and aesthetic appreciation (Nadal et al., 2010; Van Geert & Wagemans, 2020).
Important to understand is that order and complexity are no direct opposites, and can be concurrently present, either on the same or on different feature dimensions. We distinguish order from simplicity (i.e., opposite of complexity) and complexity from disorder (i.e., opposite of order). Complexity on a feature dimension allows for a broader range of order levels and a larger set of order types to be present than is the case for simplicity. For example, the safety pins in Figure 7.2a can be arranged in more qualitatively and quantitatively different ways on the size dimension than the safety pins in Figure 7.2c. However, simplicity on the size dimension does not prohibit disorder on other feature dimensions (e.g., orientation of the elements in Figure 7.2d). As explained in Van Geert & Wagemans (2020), we view order and complexity as partial complements and partial opposites. On the one hand, complexity allows order to show its potential and order helps to make highly complex stimuli ‘digestible’ and aesthetically appreciated. Order and complexity thus need each other’s presence to optimize appreciation. On the other hand, order and complexity can also relate negatively: uniformity for example indicates a low level of complexity, but also implies a high level of order on that feature dimension. Similarly, different types of symmetry may be seen as different types of order, but typically also reduce the range of complexity present in the display. Given this complex relationship between order and complexity, it is important to study their relation to aesthetic appreciation in combination, not separately (Van Geert & Wagemans, 2020).
One additional distinction that is relevant here, is the distinction between objective and subjective definitions and measures of order and complexity. Whereas objective order and complexity refer to the level and type of order or complexity that is physically present in the stimulus, subjective order and complexity entail the individuals’ perception of the order or complexity present in the stimulus (Van Geert & Wagemans, 2020). It is important to make this distinction, as research results may differ depending on how order and complexity are defined and/or measured: the concepts of objective order and complexity may for example be more easily separable from each other than the concepts of subjective order and complexity. Although many objective measures for complexity exist (for overviews, see Donderi, 2006; Van Geert & Wagemans, 2020), the set of objective measures available for order is rather limited (Van Geert & Wagemans, 2020). Since Arnheim’s (1971) seminal essay on “Entropy and art” (which was effectively about disorder and order in art), several scientists have proposed measures of order (and disorder) derived from information theory and dynamical systems theory. For instance, Redies and colleagues have defined and computed edge-orientation entropy or anisotropy in relation to preference for patterns and images of paintings (e.g., Grebenkina et al., 2018; Redies et al., 2017). However, a discussion of these would be beyond the scope of the present paper. The relative lack of objective order measures may be due to the difficulty of quantifying aspects of order other than perceptual balance or symmetry in an objective or automatized way. It is our intuition that the degree of order can be quantified for specific types of order (such as balance and symmetry) but that further research is needed to compared the degree of perceived order for different types of order. Our aim is to facilitate this research by providing a toolbox to systematically generate different types of order (e.g., different pattern types, different types of repetitions vs. changes) to compare their overall degree of perceived order (and how these interact with the number of elements, their degree of similarity and variety, etc.). Below we give an overview of different stimulus sets used in earlier research on the perception and appreciation of order and complexity that attempted to manipulate order or complexity in a parametric way.
7.1.2 Previous parametric stimulus sets in research on the perception and appreciation of order and complexity
Studies investigating the perception or appreciation of order often focused on different types of symmetry or on different measures of perceptual balance (see Figure 7.3). Chipman & Mendelson (1979) chose black and white square patterns with different types of order: unstructured, horizontal and/or vertical symmetry, diagonal symmetry, checkerboard organization, and rotational organization. Locher et al. (1998) asked participants to create designs consisting of a set of either nine circles, squares, rectangles, or leaves varying in size (3 large, 3 medium, 3 small forms per set). They investigated the changes in the center of balance as the design was completed. Wilson & Chatterjee (2005) created stimuli using the proprietary software Adobe Photoshop 7.0 and then selected a subset of these stimuli for their experiments based on a calculated balance score (i.e., the average score of eight measures of symmetry). These stimuli were later also used by Hübner & Fillinger (2016). Gollwitzer et al. (2017) generated unbroken and broken patterns to study pattern deviancy aversion in the context of social psychological research on prejudice. Although many studies in empirical aesthetics compared symmetric and asymmetric stimuli (Bertamini & Rampone, 2020), only some recent studies investigated symmetry perception or appreciation using the different systematic characterizations of symmetry in mathematics (e.g., Alp et al., 2018; Clarke et al., 2011; Kohler et al., 2016; Martin et al., 2020). Four basic symmetrical transformations are defined for two-dimensional shapes (translation, rotation, reflection, glide reflection; Grünbaum & Shephard, 1989). With these transformations, seven distinct border patterns or frieze groups (i.e., two-dimensional designs with translations in only one direction) and seventeen distinct wallpaper pattern types (i.e., two-dimensional designs with translations in two independent directions) can be specified (Grünbaum & Shephard, 1989; Thomas, 2012). Martin et al. (2020) compared beauty ratings for each of the seven frieze patterns using a comma, flag, and a filled texture as elements. Clarke et al. (2011) studied the perceptual similarity of the seventeen wallpaper pattern types. They created exemplars starting from a white noise (triangular, rectangular, or square) fundamental region and combined them into a rectangular repeating tile to produce the patterns (see also Alp et al., 2018; Kohler et al., 2016).
Studies focusing on the perception or appreciation of complexity have used a broad range of different stimulus types. Some studies used ecologically valid images and calculated statistical image properties to indicate complexity (e.g., Braun et al., 2013). Other studies used different types of fractal images (e.g., Bies et al., 2016; Spehar et al., 2016). Sun & Firestone (2021) used a measure of structural surprisal (i.e., the level of surprise associated with a shape’s skeletal structure) to categorize abstract shapes as simple and complex while controlling for the number of sides. The Matlab code to generate the shapes for that study was shared publically on the Open Science Framework.
When both order and complexity were manipulated parametrically, researchers often used random polygons (e.g., Arnoult, 1960; Attneave, 1957), black and white square patterns (e.g., Chipman, 1977; Smets, 1973), or dot patterns (e.g., Garner & Clement, 1963; Hamada & Ishihara, 1988). Attneave (1957) constructed random polygon shapes based on a varying number of turns (i.e., complexity manipulation) and manipulated them to be symmetrical or asymmetrical (i.e., order manipulation). Attneave & Arnoult (1956) provided a series of methods for the construction of random shapes. This method was later used, for example by Vanderplas & Garvin (1959), to generate random shapes of six levels of complexity (i.e., varying number of points). Smets (1973) created patterns of black and white squares in which both subjective redundancy (i.e., the percentage of correctly selected black and white elements when reproducing the pattern, related to order) and maximal information (i.e., the number of independent elements, related to complexity) were varied. These patterns were also used in studies by Berlyne (Berlyne, 1974; Cupchik & Berlyne, 1979). Chipman (1977) used similar but smaller patterns and varied structure and complexity by selecting different stimulus sets by hand. Garner & Clement (1963) produced 90 patterns by placing five dots in an imaginary 3-by-3 square matrix, with the restriction of at least one dot in each row and column, and investigated the influence of the number of patterns in the equivalence group for each pattern (i.e., the number of different patterns that can be created by rotation or reflection of the pattern) as well as symmetry. Hamada & Ishihara (1988) created rotation and reflection invariant dot patterns using imaginary rectangular and hexagonal frameworks. The dot patterns varied in the number of dots they consisted of, the order of the symmetry groups as well as the symmetry group they belonged to (i.e., cyclic and dihedral groups). In more recent years, new stimulus sets focused on symmetry and complexity manipulations. Jacobsen & Höfel (2002) constructed stimuli consisting of a solid black circle showing a centered, quadratic, rhombic cut-out and an arrangement of 86 to 88 small black triangles. Half of the patterns created were symmetric (four possible symmetry axes), the other half were not symmetric. Gartus & Leder (2013) created a new set of abstract black and white patterns using a simulated annealing stochastic optimization algorithm. They varied the number of objects (i.e., complexity manipulation) as well as the type of symmetry: no symmetry, and full and broken symmetry patterns with one, two, and four symmetry axes.
7.1.3 Existing software to generate aesthetic stimuli
7.1.3.1 FlexTiles
Westphal-Fitch and colleagues (2012) created FlexTiles, a custom-written image manipulation program, in which each of 36 tiles can be rotated to four possible orientations (0°, 90°, 180°, 270°). Participants were asked to rotate the tiles as much or as little as they liked. Patterns that emerged showed rotation, translational symmetry, bilateral symmetry along vertical axis, rotational symmetry, symmetry along diagonal axis, or local linear groupings with no overall symmetry. In later experiments, they created flawed and unflawed versions of patterns, with violations determined by color and/or orientation. Muth et al. (2019) also made use of the FlexTiles software and asked participants to produce patterns that would be liked or would be interesting. A separate group of participants rated the produced stimuli on liking, interestingness, complexity, and order. Although Muth et al. (2019) shared the stimuli used in their experiments, the FlexTiles software to recreate or adapt the stimuli has not been made openly available for use by other researchers. For OCTA stimuli created in the style of FlexTiles, see Figure 7.4.

7.1.3.2 Statistical Geometry Sampler
Güçlütürk et al. (2016) generated statistical geometric patterns using a space filling algorithm that places non-overlapping geometric shapes that monotonically decrease in size in a random fashion on a canvas (Shier, 2011; Shier & Bourke, 2013). A parameter c determining the size of the first shape element and the speed with which the size decreased was manipulated as well as the geometric shape used (i.e., circle, hexagon, square, and triangle). Although the algorithm, documented C code, and a lot of example stimuli are openly available on the website of the authors of the algorithm, and the authors mention to be open to support people interested to get started on their own images, no easy interface to create new stimuli is provided.
7.1.3.3 Aesthetic Abstract Textures Generator
One tool that does generate reproducible stimuli for use in aesthetics is the random abstract texture generator of Alvarez et al. (2021). Jean-Michel Morel, Luis Alvarez, and colleagues did design a point-and-click online tool to generate aesthetic stimuli based on composition principles and random sampling (Alvarez et al., 2021, 2015).2 This tool is meant for artists and designers to explore and test new styles, and does not allow users to manually specify the location, color, or shape of any element in the display. The shape elements are placed automatically based on the chosen composition principles and random sampling. Although this tool is very useful for the generation of reproducible aesthetic stimuli in general, it does not allow for individually controlled parametric order and complexity manipulations on different element features.
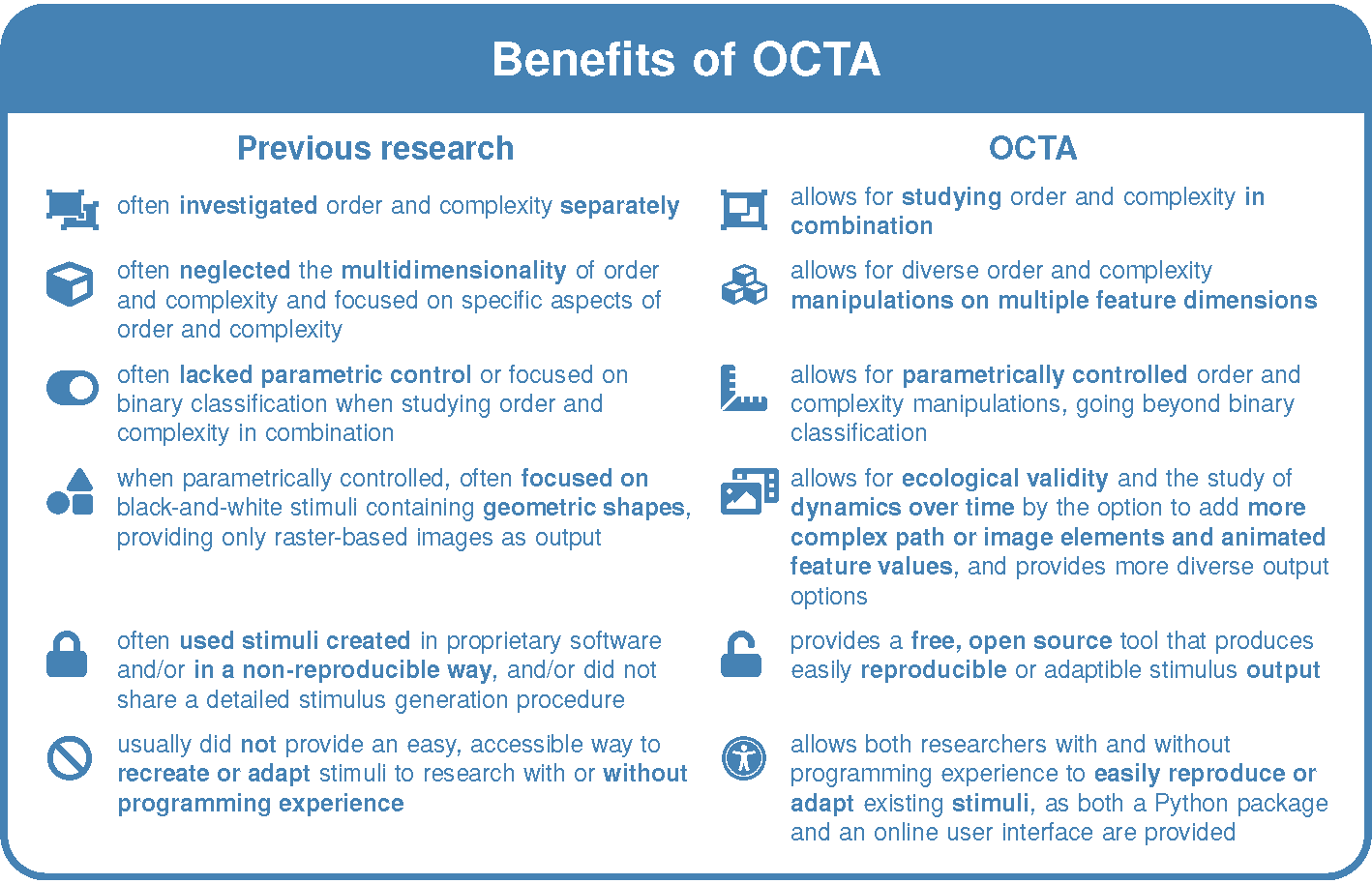
Benefits of OCTA. Figure licensed under CC BY 4.0 by the authors. Retrieved from doi.org/10.6084/m9.figshare.17740904.
7.1.4 The need for OCTA (see Figure 7.5)
As may be clear from the examples given, the existing research on the perception and appreciation of order and complexity leaves important gaps. First, most empirical work investigated the relation of order and complexity to aesthetic appreciation separately rather than in combination. Second, the relation of appreciation with complexity has been studied much more frequently than the relation with order and studies usually focused on specific aspects of order (i.e., symmetry and perceptual balance). However, many other types of organization exist (e.g., similarity grouping, proximity grouping, alternation/iteration, systematic alteration/gradient) and their influence on aesthetic appreciation has not yet been systematically studied (Van Geert & Wagemans, 2020). Furthermore, the multidimensionality (e.g., order and complexity of element colors, shapes, and sizes) of both order and complexity has often been) neglected (Nadal et al., 2010; Van Geert & Wagemans, 2020). To our knowledge, no single existing stimulus set combines systematic manipulations of order and complexity on different element features (e.g., shape, size, color, orientation). Findings based on earlier research not distinguishing between different element features may be tied to the specific aspect of order or complexity that was investigated, and may not generalize to other order or complexity dimensions.3 Third, when order and complexity were studied in combination, researchers often focused on a binary classification in high and low order and/or complexity rather than more fine-grained order or complexity manipulations4, or more ecologically valid stimuli were used but then parametric control over both order and complexity dimensions was lost (e.g., Nadal et al., 2010; Van Geert & Wagemans, 2021). Findings based on this last type of research, using less controlled stimuli, require replication with a more parametrically controlled stimulus set where both order and complexity of the stimulus can be manipulated as independently as possible.5 Fourth, when parametrically varied stimulus sets were used, the focus was often on black-and-white stimuli containing geometric shapes. Fifth, the stimuli used in aesthetics research were often created using proprietary software, in a non-reproducible and non-adaptable way, or not openly available to the research community, or the researchers did not share enough details concerning how the stimuli were generated. Sixth, in case a detailed stimulus generation procedure was provided, stimuli could not be recreated or adapted easily without programming experience. Therefore, research on order and complexity would benefit from an easy way to create standardized stimuli varying qualitatively and quantitatively in many different aspects of order and complexity, with options for increased ecological validity but without losing parametric control.
The Order & Complexity Toolbox for Aesthetics (OCTA) is such a free, openly available tool and creates many opportunities to investigate order and complexity in a standardized and multidimensional manner, with a focus on multi-element displays. With OCTA, one can manipulate and measure order and complexity in a systematic way, and study their effects in combination. OCTA acknowledges the multidimensionality of order and complexity by allowing separate manipulations of different element features (e.g., shape, size, color, orientation). It allows for parametric control on many different stimulus and element features. It also acknowledges the potential of research on the dynamics of order and complexity by including animation options for several element features including color, size, and orientation. To provide more ecological validity, OCTA makes it possible to use of images or path elements6 in a stimulus. OCTA is freely available, open source, and enables users to create reproducible, code-based stimulus sets that are easily adaptable or extendible. The standard vector-based output is ideal for experiments on the web and the creation of dynamic interfaces and stimuli, while raster-based output is possible as well. Furthermore, OCTA is accessible to both researchers with and without programming experience, as both a Python package and an online user interface are provided. With OCTA being fast, flexible, and transparent, we strongly believe that OCTA will facilitate reproducible stimulus construction and experimental design in research on order, complexity, and aesthetics. In addition, OCTA can be a very useful tool to investigate visual perceptual organization, to create visual stimuli for any type of experimental or cognitive task, or even to create digital art.
7.2 The OCTA toolbox as a Python package and a Shiny application
The octa package is a Python package developed in Python 3.8 (Van Rossum & Drake Jr, 2009) and is available (on the Python Package Index or on GitHub) as open-source software under the GNU Lesser General Public License (Version 3) as published by the Free Software Foundation.7 We chose to create this toolbox in Python as Python is a powerful and popular open source programming language for which a large online community is available. Elaborate documentation on the octa Python package is available, offering a step-by-step introduction to the full functionality of the OCTA toolbox. To get users started, a website with example stimuli (see dynamic stimuli here) and the corresponding code is provided. For users who want to dig further into the toolbox, detailed function documentation is available. Besides developing the Python package, we also developed a Graphical User Interface for the OCTA toolbox, in the form of a Shiny application.8 The procedure described below will be for using the Python package, but most aspects are similar in the Shiny application (we will indicate the most important differences in text). Additional instructions for the use of the Shiny application are provided in the app itself.
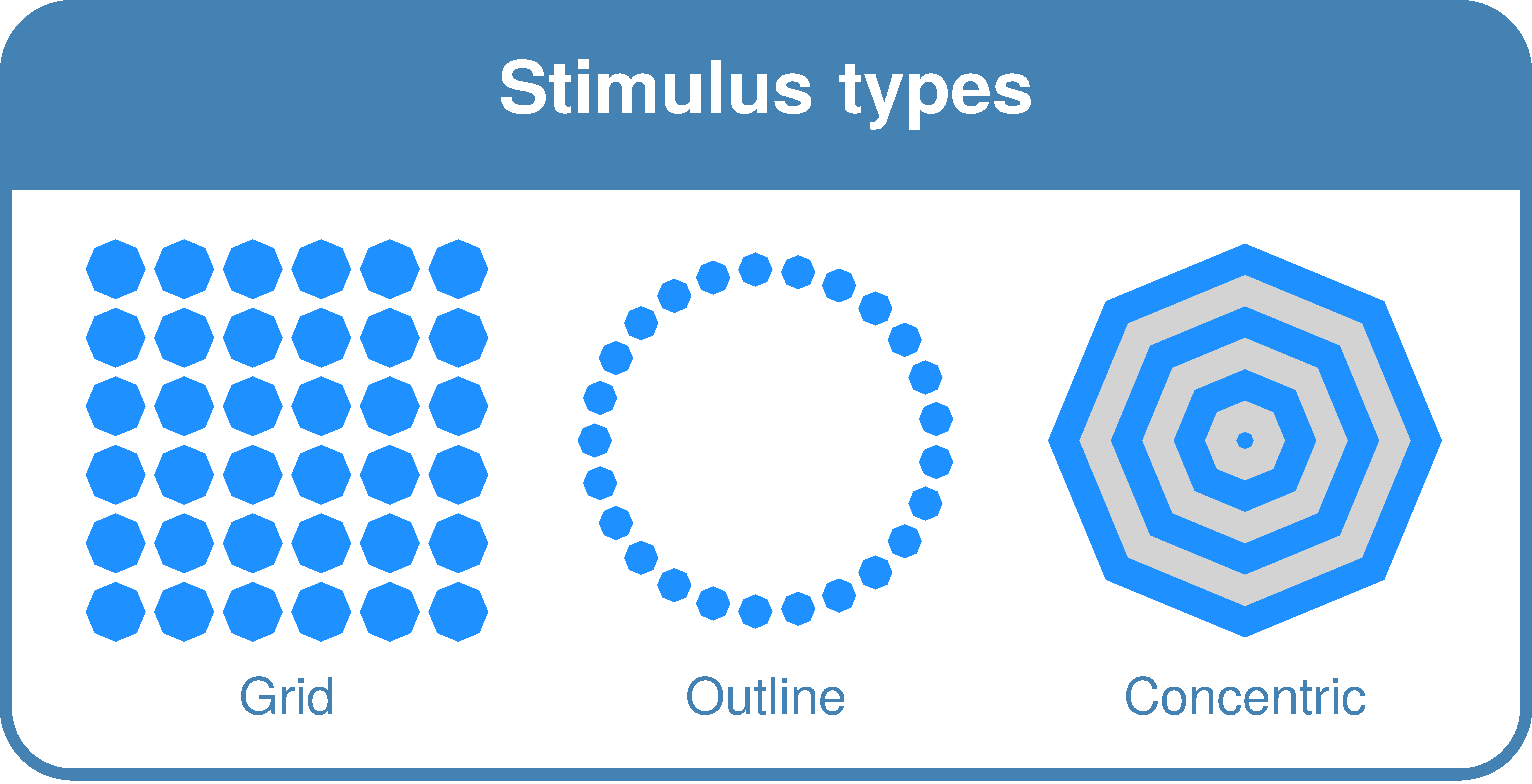
Figure 7.6 gives an overview of the terminology used in OCTA.9 In OCTA, you can create stimuli consisting of multiple elements. First, the user specifies the type of stimulus they want to create (i.e., Grid, Outline, Concentric; see Figure 7.8) as well as the general stimulus features they want to adapt (e.g., stimulus size, background color or shape, stimulus orientation). Second, they can replace the default position pattern for the stimulus type by a custom one (e.g., sine grid, custom shape, custom positions). Third, the element feature patterns can be specified by defining pattern type, pattern direction, and pattern values per element feature. Fourth, position, element, and feature deviations can be added. Finally, the user can save the resulting stimulus in the preferred formats: as a vector-based image (SVG), as a raster-based image (PNG, JPG, PDF, or TIFF), and/or as a computer-readable file (JSON). The SVG format is recommended for online use, as it has the same quality at all viewing sizes and keeps the possibility for animated element and stimulus features. The JSON output can be used to recreate the stimulus in Python using the OCTA toolbox without the original code (using the LoadFromJSON function).10 In the Shiny app, the user can also view or download the Python code needed to reproduce the current stimulus with the octa package in Python.


7.2.1 Step-by-step guide to creating a stimulus using OCTA (see Figure 7.7)
The following section gives a more detailed overview of the steps of creating a stimulus (set) in OCTA.11 For a visual summary of the different steps needed to create a first stimulus in OCTA, consult Figure 7.7.
7.2.1.1 Step 0. Load the octa package in Python
To start using the octa Python package, install octa as well as its dependencies (svgwrite, svg.path, svgpathtools, svgutils, jsonpickle, html2image, svglib, reportlab, colour, and IPython). Once everything is installed, it can be helpful to import specific functions from the octa package. In the Shiny app, this step is unnecessary as all required packages are loaded automatically. Furthermore, the user can download the Python code from the Shiny app and copy it to Python to import the functions from the octa package necessary for a specific stimulus.
7.2.1.2 Step 1. Specify a stimulus type
The first step when creating a stimulus is to define the type of stimulus one wants to create: a Grid stimulus, an Outline stimulus, or a Concentric stimulus (see Figure 7.8).12 These stimulus types correspond to frequently used stimulus types in the literature. For instance, Grid stimuli have been used by Garner & Clement (1963) and Chipman & Mendelson (1979), and have formed the basis for FlexTiles and many stimuli in visual search tasks. Outline stimuli could form the basis for hierarchical stimuli like those used by Navon (1977), Poirel et al. (2006), and Krakowski et al. (2016). For Concentric stimuli, see for instance Gollwitzer et al. (2017). Whereas a Grid stimulus requires a specified number of rows and columns, Outline or Concentric stimuli require a specified number of elements.13 If desired, the user can specify additional arguments to customize the stimulus. The following features of the stimulus as a whole can be specified: spacing between rows and columns (in case of a Grid stimulus), shape and shape bounding box (in case of an Outline stimulus), horizontal and vertical margin (when automatic sizing method is used), stimulus size (when fixed size is needed), background color, background shape, stimulus orientation, mirror value for the stimulus as a whole, mask to apply for the stimulus as a whole, and link, class label, and id label for the stimulus. By default, stimuli will be autocentered with a horizontal and vertical margin of 20 units in the current user coordinate system (i.e., user units), have a white background color, and an orientation of 0°. The Grid category has a default row and column spacing of 50 user units, and the Outline category by default has a circular shape with a bounding box of 150 by 150 user units. For more information on all stimulus features, please consult the online documentation. In the Shiny app, additional stimulus features can be specified under the tab ‘0. Add stimulus features’. The general stimulus type has been merged with the other position pattern options however, and can be changed under the tab ‘1. Add position pattern’.
7.2.1.3 Step 2. Specify element positions
Having created the stimulus, the resulting x and y coordinates for the element positions can be requested via . The position of an element is determined by the center of the element’s bounding box (i.e., the rectangle ‘bounding’ the size of the element shape). The default position patterns used for Grid, Outline, and Concentric stimuli are a rectangular grid with a row and column spacing of 50 user units, a circle outline with radius 150, and identical (0,0) positions, respectively. The user can replace the default position pattern for the stimulus type by a custom one (e.g., a sinewave-shaped grid, a custom shape outline, random positions within a specified rectangle, manually specified positions). Figure 7.9 gives an overview of all currently available position pattern functions.14 Important to note is that any custom set of positions can be defined using the CreateCustomPositions function. For more information on all position pattern definitions, please consult the online documentation. In the Shiny app, the element positions can be specified under the tab ‘1. Add position pattern’.

7.2.1.4 Step 3. Specify patterns and pattern values for different element features
Once the stimulus features and element positions are specified, the pattern types, pattern directions, and pattern values for the different element features can be adjusted. The patterns can be applied to the following element features: shapes, boundingboxes, fillcolors, orientations, borderwidths, bordercolors, opacities, mirrorvalues, links, classlabels, and idlabels (see Element features and Figure 7.12). In Grid and Outline stimuli, one value per element feature is repeated across all elements in the stimulus by default. In Concentric stimuli, a pattern with two fillcolors is repeated across all elements in the stimulus by default, and the boundingbox sizes follows a decreasing gradient across elements. Available pattern types (see Figure 7.10)15 include pattern repetition (Repeat), element repetition (ElementRepeat), mirror symmetry (Mirror), and a gradient from a start value to an end value (Gradient). In Grid stimuli, these patterns can be applied according to the following pattern directions: across elements, across rows, across columns, across the left diagonal, across the right diagonal, and across layers (see Figure 7.11). In addition, more complex patterns can be constructed using the TiledGrid and TiledElementGrid options. Whereas a TiledGrid copies the feature values in a source grid a specified number of times in the row and column directions, a TiledElementGrid copies each element in the source grid a specified number of times in the row and column directions. Finally, a random application of the values for the element feature across the elements is possible too (RandomPattern). By default, the pattern values in the RandomPattern are repeated until the length is equal to the number of elements in the stimulus. Optionally, a list of frequencies can be provided to determine how many times each pattern value has to be present. In Outline and Concentric stimuli, it is strongly advised to apply patterns across elements (as other pattern directions will not be distinguishable in Outline and Concentric stimuli). In the Shiny app, the feature patterns can be specified using the tabs under ‘2. Add feature patterns’. Some predefined pattern values are provided for each element feature, but custom pattern values can be specified too.

7.2.1.4.1 Element features (see Figure 7.12)
7.2.1.4.1.1 Shapes
Available element shape types are geometric shapes, i.e., Ellipse, Rectangle, Triangle, Polygon(n_sides), RegularPolygon(n_sides); more complex path elements16 based on a provided path string or an existing SVG file, i.e., Path(path, xsize, ysize), PathSvg(source); images based on a provided filename or source url, i.e., Image(source), FitImage(source); and text elements17, i.e., Text(text). Keep in mind that for the order and complexity measurements, the shapes argument only takes the shape type into account and does not distinguish between different polygons, different paths, different images, or different texts.18 Currently no built-in animation options are available for the shape feature, but it is possible to include dynamic image files (e.g., dynamic SVG or gif file) as shape values in the stimulus. Also in the Shiny app, it is possible to specify custom shapes to use in the stimulus, including Image and PathSvg shapes that are publicly accessible online. It is however not possible to use local files when working with the online Shiny app.
7.2.1.4.1.2 Boundingboxes
Boundingboxes are always rectangular but do not have to be squared. Boundingbox values are defined in user units and can be provided as follows: (xsize, ysize). Although currently no built-in animation options are available for the boundingbox feature, it is possible to either generate separate stimuli and combine them in time afterwards, or to include dynamic image files (e.g., dynamic SVG or GIF file with shape changing in size) as shape values in the stimulus. Shapes will take their maximal size possible within the specified boundingbox, taking into account shape definitions (e.g., the Image shape type will retain original aspect ratio of the image, whereas the FitImage shape type will fit the image to the boundingbox without taking original aspect ratio into account).19
7.2.1.4.1.3 Fillcolors
Besides static uniform colors defined based on their hexadecimal color code or color name, the user can specify a radial or linear color gradient with multiple colorvalues (i.e., radial, horizontal, vertical, diagonal) or dynamic fillcolors by setting a new color (i.e., ‘set’) when a certain action occurs (e.g., when the element is clicked) or by animating the color value (i.e., ‘animate’). Fillcolors are not visible for image elements.
7.2.1.4.1.4 Orientations
Orientations are defined in degrees. Besides static orientation values, dynamic definition of orientations is possible (i.e., ‘set’ or ‘animate’).
7.2.1.4.1.5 Borderwidths
Borderwidths are defined in user units. Besides static borderwidth values, dynamic definition of borderwidths is possible (i.e., ‘set’ or ‘animate’). Borderwidths are not taken into account when a shape is fit to a particular boundingbox value, which means that half of the borderwidth will fall outside of the specified shape and thus potentially outside of the specified boundingbox (as the borderwidth is centered around the shape border). Keep in mind that the default bordercolor is transparent, so bordercolor needs to be set for the borderwidth value to have a visible effect. In addition, borderwidths are not visible for image elements and may behave unexpectedly for path elements.20
7.2.1.4.1.6 Bordercolors
Besides static uniform bordercolors defined based on their hexadecimal color code or color name, the user can specify a radial or linear color gradient with multiple bordercolor values (i.e., radial, horizontal, vertical, diagonal) or dynamic bordercolors by setting a new color (i.e., ‘set’ ) when a certain action occurs (e.g., when the element is clicked) or by animating the color value (i.e., ‘animate’). Bordercolors are not visible for image elements. Keep in mind that the default borderwidth is zero, so borderwidth needs to be set for the bordercolor values to have a visible effect.
7.2.1.4.1.7 Opacities
Opacities are defined between 0 (no opacity) and 1 (full opacity). Besides static values, dynamic definition of opacities is possible (i.e., ‘set’ or ‘animate’).
7.2.1.4.1.8 Mirrorvalues
As element shapes can be mirrored along the horizontal and/or vertical axis, or not be mirrored, this element feature can take any of four different values: ‘none’, ‘horizontal’, ‘vertical’, ‘horizontalvertical’. Currently no built-in animation options are available for the mirrorvalue feature, but it is possible to either generate separate stimuli and combine them in time afterwards, or to include dynamic image files (e.g., dynamic SVG or GIF file with shape changing in mirrorvalue) as shape values in the stimulus.
7.2.1.4.1.9 Links
A custom hyperlink can be added to every element in the stimulus. This entails a hand cursor shown when the viewer hovers over that specific element, and the opening of a hyperlink when the element is clicked.
7.2.1.4.1.10 Classlabels and idlabels
Although classlabels and idlabels do not have a directly visible effect on the resulting element, they can be used to add additional JavaScript actions or CSS style changes to individual elements (using the idlabel) or to a group of elements (i.e., all elements with the same classlabel). This method can, for example, be used to add sounds when hovering over an element or when an element is clicked.
7.2.1.4.1.11 Data
Data is a hidden element feature not meant for direct user interaction. It stores the additional arguments given to any of the shapes (e.g., the number of sides for Polygon objects, the source argument for Image objects). This element feature may become important when calculating order and complexity measures within the OCTA toolbox, to distinguish between polygons with a different number of sides, different path definitions, different text elements, or images with different sources.
7.2.1.5 Step 4. Add deviations and calculate measures
Once all element feature patterns are specified as desired, the user can add position, element, or feature deviations to decrease the order and/or increase the complexity of the stimulus. Figure 7.13 gives examples of the position, element, and feature deviations that can be added. Although most of these deviation types affect both objective order and objective complexity, some manipulations specifically target either order or complexity. Position, element, and feature deviations are saved separately from the original patterns used to create the stimulus. If multiple deviations are added, later deviations could overwrite earlier deviations if they concern the same position, element or element feature. In the Shiny app, deviations can be added under the tab ‘3. Add deviations’. Within this tab, position and element deviations are bundled under ‘Position deviations’ and element feature deviations are displayed under ‘Feature deviations’.

7.2.1.5.1 Position deviations
Random jitter or specified deviations can be added to the element positions. Although the impact of position deviations is dependent on the specific deviations added as well as the position pattern used as starting point, they generally increase objective complexity in the positions used in the stimulus (i.e., they increase the variety of positions present in the stimulus). Element or feature complexity stays unchanged when deviating position only. Whether the position deviations influence objective order in positions, elements, or features depends on the specific deviation.21 For normally distributed or uniformly distributed position jitter, one can specify whether the jitter needs to be applied to the x coordinates, y coordinates, both axes equally, or both axes independently using the axis argument. In the case of uniformly distributed jitter, the user specifies a minimum and a maximum value (min_val and max_val). In the case of normally distributed jitter, the user specifies mean (mu) and standard deviation (std). Default values for axis, distribution, min_val, max_val, mu, and std are ‘xy’, ‘normal’, -1, 1, 0, and 1, respectively. To add specific position deviations, the user specifies the element ids (starting from 0 until n_elements - 1), x offsets and/or y offsets for each of the elements to which a deviation relative to the predetermined position needs to be added. Element id needs to be given an integer value or a list of integer values. X and y offsets can be numeric values or a list of numeric values.
7.2.1.5.2 Element deviations
To add element deviations, it is possible to remove a set of random or specified elements from the display, to swap the positions of distinct elements, or to randomize the order of all elements in a particular direction. Bringing an additional element into the pattern is possible as well, but requires the user to add an additional element in the stimulus definition and in the definition of the stimulus positions. Swapping or randomizing the position of distinct elements in the display decreases objective element order, but leaves objective position, element, or feature complexity unchanged. If also non-distinct elements would be swapped or randomized, the objective element order may stay unchanged. Removing elements does complicate the position pattern and potentially reduces element or feature complexity, but more generally also decreases element and feature order.
7.2.1.5.3 Feature deviations
To add feature deviations in the stimulus, it is possible to change a feature value for a number of random or specified elements, to swap the feature values for a number of random pairs of (distinct) elements in the display, to randomize the order of all feature values in a particular direction, or to jitter any of the numeric feature values across all elements. Swapping or randomizing the position of distinct feature values in the display decreases objective order for the feature dimensions involved, but also increases objective element complexity. Changing a feature value to a value that is not yet in the pattern values for that feature or jittering numeric feature values will additionally increase objective feature complexity. An advantage of adding feature deviations is that order can be distorted on one feature dimension specifically but preserved for other feature dimensions (contrary to what is the case with element deviations).
7.2.1.5.4 Order and complexity measures and manipulations
Although deviations are one way to increase or decrease different types of order and complexity in the stimulus, other approaches are possible too. Figures 7.14 and 7.15 give an overview of some order and complexity manipulations that are possible in OCTA. Figure 7.16 lists the order and complexity measures available in OCTA.
7.2.1.5.4.1 Manipulating order
Position order can be changed qualitatively by changing the type of position pattern. Element (and feature) order can be changed qualitatively by changing the different element feature pattern types and directions.22 To induce quantitative changes in order, the user can swap the positions of distinct elements or randomize the elements in the stimulus (which keep element complexity level constant), or add any other element or feature deviations (but these other deviations may influence element or feature complexity as well; cf. Step 4. Add deviations). The user can also make stimulus features and element features (in)congruent to impact the order level of the stimulus. In addition, the congruency of patterns, pattern types, or pattern directions across feature dimensions can be adapted.23
7.2.1.5.4.2 Manipulating complexity
Qualitative changes in complexity can be achieved by changing the feature dimension on which the complexity is present (e.g., shape, color, or size complexity). Quantitative element complexity changes can include (a) changing the number of visible elements present in the stimulus (i.e., by removing elements or by changing the position pattern of the stimulus), (b) manipulating the variety of elements (i.e., by including more pattern values on a feature dimension, by choosing more diverse pattern values, by adding feature deviations, or by changing the congruency of patterns across feature dimensions), (c) changing the complexity (familiarity, unintelligibility, etc.) of individual feature pattern values (e.g., use complex path shape instead of rectangles), or (d) changing the complexity of individual stimulus features. Position complexity can be changed quantitatively by adding random position jitter or structured position deviations (cf. Position deviations).
7.2.1.5.4.3 Measuring order and complexity
OCTA provides some basic functionality to measure aspects of order and complexity in the created stimulus. When it comes to complexity measures, it is possible to calculate (a) the number of elements present in the display (Number or N), (b) how many different types of elements are present in the display based on the feature dimensions specified (Level of Complexity based on Elements or LOCE), (c) how many different features are present across all feature dimensions (Level of Complexity or LOC), and (d) how many different feature dimensions have more than one feature value (i.e., have non-identical values; Level of Complexity based on Identity or LOCI). For order, the user can request the applied patterns, pattern types, and pattern directions across all feature dimensions; check whether all specified feature dimensions have congruent patterns, pattern types, or pattern directions; calculate how many specified feature dimensions have congruent patterns, pattern types, or pattern directions; calculate the number of deviant elements that are present given the specified feature dimensions (e.g., by added element or feature deviations); and calculate the number of deviant positions that are present in the stimulus (i.e., by added position jitter or specified position deviations). In the Shiny app, order and complexity measures can be calculated under the tab ‘4. Calculate measures’. Also in the Shiny app the user has the option to specify which element features to take into account when calculating the measures.

7.2.1.6 Step 5. Generate the stimulus, show it on screen, and save to the desired output format
Finally, the user can save the resulting stimulus in the preferred format: as a vector-based image (SVG), as a raster-based image (PNG, JPG, PDF, or TIFF), or as a computer-readable file (JSON). The SVG format is recommended for online use, as it has the same quality at all viewing sizes and keeps the possibility for animated element and stimulus features. For raster-based image output, a scale value can be added to increase the quality when starting from a very small stimulus that would otherwise have pixel artefacts.24 The JSON output can be used to recreate the stimulus in Python using the octa package without the original code (using the function). In the Shiny app, the user can download the stimulus as a vector-based SVG image or as a raster-based PNG or PDF image, the JSON output, or the Python code needed to reproduce the current stimulus with the octa package in Python. Besides, the Shiny app user can view the Python code (without the octa import statements), the raw SVG code, and the JSON code in the app itself.
7.3 Discussion and conclusion
With the OCTA toolbox, it is possible to study order and complexity in combination. It acknowledges the multidimensionality of order and complexity and provides the tools to manipulate and measure order and complexity in several ways and on different feature dimensions.25 The possibility to add more complex shapes and images in the stimulus enables the user to find their own balance between ecological validity and experimental control. As online testing becomes ever more common, vector-based OCTA stimuli are ideal for online use and allow room for dynamical features. The OCTA toolbox however is not constrained to vector-based output as it still allows for saving the stimuli as raster-based image formats. Importantly, OCTA provides a reproducible way of creating stimuli, as all OCTA code is open source, and tools are made available to reproduce the stimuli, either based on the original seed used and the original code or with the original seed used and a JSON file. Furthermore, as both a Python package and an online app are provided and a multitude of documentation and example stimuli are provided, using OCTA is possible for both researchers with and without programming experience, making it a widely accessible tool. Below we discuss some more advanced uses of OCTA, potential applications, and give advice on how to start using OCTA.
7.3.1 Using animated stimulus and element feature values
One of the big advantages of the OCTA toolbox being vector-based, is the option to animate a diverse set of stimulus and element features either directly within the OCTA toolbox (i.e., using SVG animation to animate stimulus orientation and element fillcolors, orientations, borderwidths, bordercolors, and opacities) or after the OCTA stimulus has been created (i.e., using some additional CSS or JavaScript code, making use of the class and id labels that can be added to specific elements within OCTA stimuli and to OCTA stimuli as a whole).
Within the OCTA toolbox, a wide range of animation options is available: for example, animations initiated by clicking or by a specified starting time, animations including discrete steps or continuous change in feature values, one-time or indefinitely repeating animations. For use of animated feature values in OCTA, have a look at some dynamic stimulus examples or try out some of the animated example feature values in the OCTA Shiny app. For a more detailed reference on animation options in the SVG language, consult the SVG documentation on animation by The World Wide Web Consortium or Mozilla, or the documentation of the svgwrite Python package that is used within the octa Python package.
For more information on how to add CSS or JavaScript animations to SVG images based on class or id labels once the OCTA stimulus has been generated, consult the general documentation on CSS or JavaScript animations by W3Schools or search the internet for more specific tutorials on SVG animation using CSS or JavaScript. For a very simple demo using OCTA stimuli, consult the part on adding stimulus class and id labels in the OCTA documentation (or go directly to the example).
7.3.2 Creating sets of stimuli
Depending on the research question at hand, one can create differently controlled stimulus sets using OCTA. For example, a researcher interested in investigating the influence of the level of order on perception and appreciation of an image under different levels of complexity may create stimuli varying in order level but keeping order type, complexity level and complexity type constant at a smaller number of values. A researcher interested in investigating the generalizability of particular findings concerning order, complexity, and aesthetic appreciation may create stimuli keeping order and complexity levels and types constant but varying the pattern values used in each of the feature dimensions (e.g., fillcolors, boundingboxes, shapes). Furthermore, a researcher interested in studying to what extent and in which way order and complexity on different feature dimensions influence the perception and appreciation of an image, may create stimuli varying the type of complexity present (e.g., number and variety of fillcolors, boundingboxes, or shapes) and keeping order type, order level, and complexity level constant.26 Researchers investigating perceptual grouping principles including proximity and different types of similarity may use the OCTA toolbox to create congruent and incongruent stimuli, vary row and column spacing in Grid stimuli, or vary the absolute feature values used to investigate the generalizability of the grouping strengths beyond typically used feature values (e.g., black-colored circular elements in the commonly used dot lattices). Moreover, researchers concerned with ecological validity of earlier findings may create equivalent stimulus sets with more abstract and more concrete shapes relevant to daily life (e.g., comparing a standard circle and a circle looking like a button, or comparing a standard triangle and a triangle looking like a tent). These are only examples of stimulus sets that could be created, as the OCTA toolbox gives researchers a very elaborate range of options that can be combined in any way preferred.
When creating sets of stimuli, it may be advisable to use the octa Python package rather than the app, as using Python directly will give you more opportunities to use loops and create multiple stimuli at once. This does not hold users back to first create one of the stimuli in the Shiny app, and then copy the code to Python for creating the complete set of stimuli. For researchers more familiar with R than with Python, the reticulate package (Allaire et al., 2017) can be very useful to interact with the octa Python code when creating and saving the combinations of parameter values for the stimuli in R rather than in Python directly.
7.3.3 Applications
Although OCTA has originally been created to study order and complexity in the context of empirical aesthetics, the toolbox can be used for generation of static or dynamic stimuli in a much broader field of research using visual stimuli as well as in non-academic use contexts. Examples of some research fields that could benefit from the use of OCTA are perceptual organization (e.g., grouping principles), symmetry detection, local-global processing and part-whole relationships, texture perception, visual search, visual illusions, perceptual averaging, ensemble perception, other types of visual perception research (for a review of many of these topics, see Wagemans, 2018), creativity, joy of ordering, aesthetic appreciation in general, and many more (see Figure 7.17). For example, although OCTA is not built with a focus on different types of symmetry specifically, all four basic two-dimensional symmetry operations (rotation, translation, reflection, and glide reflection) are at least in some form automatically available in OCTA27, and the seven frieze patterns as well as the 17 wallpaper patterns can be created using OCTA.28 In sum, OCTA can be a useful tool in any type of research using visual stimuli, and even to generate digital art (for some more examples, see Figure 7.1). In addition, OCTA stimuli can be used in many different kinds of tasks (rating, pairwise comparison, ranking, sorting, detection, construction, adjustment, etc., for a review of many of these tasks, see Palmer et al., 2013). For some experiment demos in jspsych (de Leeuw, 2015), consult the linked webpages (demos, code). Preliminary versions of OCTA are currently already being used both in research on the perception and appreciation of order and complexity (including order and complexity variations in shapes, boundingboxes, fillcolors, and number of elements, Van Geert, Warny, et al., in preparation; Van Geert, Hofmann, et al., in preparation) and in research on the proximity principle in perceptual organization (including manipulations of row spacing and column spacing, Van der Hulst et al., in preparation).
7.3.4 Advice on starting to use OCTA
Although learning to work with a new tool can lead to some cold feet, the online application as well as all the additional resources (e.g., manual, example stimuli, detailed function documentation; for an overview, visit elinevg.github.io/OCTA/) help users along the way. As OCTA is a new tool, feedback is welcomed and there are many opportunities for further development (e.g., additional position patterns and deviation options, additional animation options, option to create multiple stimuli at once). We do believe however that the current functionality already provides an immense array of options unexplored in aesthetics and visual perception research so far, and invite readers to explore the options29 in the app (for starting users) or the Python package (for researchers with some prior Python programming experience; on the Python Package Index or on GitHub).30
7.4 Open practices statement
The octa Python package is available (on the Python Package Index or on GitHub) as open-source software under the GNU Lesser General Public License (Version 3) as published by the Free Software Foundation. The following webpage collects all additional resources concerning the OCTA toolbox: https://elinevg.github.io/OCTA/, including the Shiny app, the OCTA manual, the octa function documentation, example stimuli created in OCTA, demo experiments using OCTA stimuli, and more. When using either the octa Python package or the OCTA Shiny app in your (academic) work, please cite this paper to acknowledge the authors.
We will use octa in small letters when referring specifically to the Python package and OCTA in capital letters when referring to the toolbox in general, regardless of whether it concerns the Python implementation or the Shiny app.↩︎
The same authors also created an abstract shape generator which may be of interest to the readers.↩︎
This will always be the case to some extent but experimental control and generalization are made much easier in OCTA because it provides easy handles to create and test systematically many more variations.↩︎
Whether a more continuous manipulation of order levels also leads to a continuous change in perceived order is an empirical question that can be addressed using the OCTA toolbox.↩︎
Although it is important to study order and complexity in combination (i.e., in a factorial design taking into account both order and complexity), we do believe it is important to study order and complexity as independently as possible (i.e., in a non-confounded way, separating both factors as much as possible within the same experiment).↩︎
Path SVG elements can be used to draw any type of lines, curves, or custom shapes based on a combination of straight or curved lines. For more information on how to define paths, have a look at these online tutorials by and .↩︎
To make full use of octa, Python 3.6 or higher is required, and the toolbox depends on the Python packages svgwrite (Moitzi, 2021), svg.path (Regebro, 2021), svgpathtools (Port, 2021), svgutils (Telenczuk, 2021), jsonpickle (Aguilar, 2021), html2image (vgalin, 2021), svglib (Gherman, 2021), reportlab (Robinson et al., 2021), colour (Lab, 2021), and IPython (Pérez & Granger, 2007). In addition, Google Chrome (Windows, MacOS) or Chromium Browser (Linux) needs to be installed to be able to generate PNG, JPG, or TIFF raster images based on the stimulus.↩︎
When using either the octa Python package or the OCTA Shiny app in your (academic) work, please cite this paper to acknowledge the authors.↩︎
We realize that it is quite difficult to understand and remember this terminology. This difficulty follows from the wide range of stimulus variations we want OCTA to be able to generate. First-time users might be put off by this difficulty. However, we suggest you try working with the toolbox to familiarize yourself with the options, and then Figure 7.6 and the descriptions in the main text become a handy reference in case you want to develop a more refined understanding all the available options or gain more experience with them.↩︎
Keep in mind that to reproduce the exact same stimulus, one needs to set a seed before running (each line of) the OCTA Python code and also keep this seed (these seeds) along with the JSON file in case any randomization procedures are used in the stimulus generation. In addition, the safest way to ensure reproducibility is by keeping track of the code, seed, and OCTA toolbox version you used to create your stimuli.↩︎
In line with footnote 10, the following description of the available options (especially in steps 2-4) will probably be overwhelming for most first-time users. The best way to come to grips with this is to first check the figures (especially Figures 7.7-7.15) for a quick visual impression of the available options and then to read the accompanying text for more details about specific possibilities. Again, this description will become more understandable and useful after having gained some initial experience with OCTA.↩︎
These options were chosen to allow the user to create a broad range of stimuli with only a limited number of specified stimulus types. The set of specified stimulus types is partially arbitrary and necessarily incomplete, and can be expanded in later generations of the toolbox based on user feedback or requests.↩︎
The stimulus types Outline and Concentric are defined as Grid stimuli with the number of rows equal to one and the number of columns equal to the number of elements.↩︎
These options were chosen to allow the user to create a broad range of stimuli with only a limited number of specified position definitions. The set of specified position definition functions is partially arbitrary and necessarily incomplete, but can be expanded in later generations of the toolbox based on user feedback or requests.↩︎
These options were chosen based on the currently available literature using different pattern types, e.g., Chipman & Mendelson (1979), and to allow the user to create a broad range of stimuli with only a limited number of specified pattern types. The set of specified pattern types is necessarily incomplete, but can be expanded in later generations of the toolbox based on user feedback or requests.↩︎
When providing a path definition or SVG file, keep in mind that the path or file may contain margins, making the visible result smaller than the defined boundingbox size. Correctly fetching a path from an existing SVG file may fail in case the SVG file contains multiple paths, no paths, or paths are specified differently than expected (e.g., including margins).↩︎
Text elements are an experimental feature of the OCTA toolbox. The sizing of the text elements is optimized for a single capital letter to fit in the boundingbox provided.↩︎
For example, in an OCTA stimulus containing two different images as image elements, the number of shape types used will be one. To take into account the number of different images, polygons, paths, or texts used, one can add the ‘data’ argument to the element features used in the order and complexity measurements.↩︎
As specified in footnote 12, when providing a path definition or SVG file, keep in mind that the path or file may contain margins, making the visible result smaller than the defined boundingbox size. Furthermore, the sizing of the text elements is optimized for a single capital letter to fit in the boundingbox provided.↩︎
Related to footnote 12, when providing a path definition or an SVG file containing a path definition, the path definition may contain margins, making the visible result smaller than the defined boundingbox size. In addition, the path may be defined on another size than it is scaled to, and the borderwidth will be applied to the original size, making the visible borderwidth often smaller than intended. A correct path definition and a borderwidth value custom to the original path boundingbox is thus key to get a correct borderwidth for path elements.↩︎
One may argue that position deviations decrease the objective order in the positions, but this may not always be the case. For example, when , these positions deviations may only alter—or in some cases even increase—the structure and organization of the positions present in the stimulus.↩︎
Be aware that some feature pattern changes may also impact element complexity because of emerging (non-)congruency between different feature patterns.↩︎
Keep in mind that changes in pattern congruency may simultaneously influence element complexity.↩︎
It is also possible to add this scale value to the SaveSVG function, to scale the vector-based image to the preferred size.↩︎
It is a conscious choice to not provide a full set of commonly used order and complexity measures within OCTA and only keep it to order and complexity measures directly deriving from the stimulus construction procedure. Calculating additional complexity measures can be useful, for which other tools already exist, e.g., imagefluency, Mayer (2021), described in Mayer & Landwehr (2018b) and Mayer & Landwehr (2018a); image spectral slope, fractal dimension and Shannon entropy as described in Mather (2018) and Mather (2020); PHOG measures described in Braun et al. (2013); and edge-orientation entropy as described in Redies et al. (2017). The user can use the vector- or raster-based image output to calculate these additional measures.↩︎
One prerequisite for studying the multidimensionality of order and complexity may be finding equivalent levels of change on different feature dimensions.↩︎
Rotation can be achieved using the orientation feature dimension, translation in horizontal and vertical directions is possible using the col_spacing and row_spacing parameters in the Grid stimulus type and translation in any direction is possible using custom position definitions; reflection can be achieved using the mirrorvalue feature dimension; and glide reflection can be achieved using a combination of translation and reflection manipulations.↩︎
As OCTA currently builds mostly from rectangular grids, generating wallpaper patterns starting from these requires less customization (e.g., custom position definitions) than creating wallpaper patterns starting from other grid types. One potential avenue for further development of the OCTA toolbox is adding additional grids and related pattern types, to make the creation of some of these wallpaper patterns more straightforward in OCTA.↩︎
With some additional JavaScript, it is even possible to add sounds to specific elements or stimuli as a whole and thus to create multimodal stimuli (cf. class labels and id labels in the online documentation).↩︎
To start working with the octa Python package, it can be helpful to copy Python code from the Shiny app, the manual or the example stimuli in Python and start from there.↩︎